Il y a une chance sur 4 milliards 100 millions que dans un groupe de 120 personnes, réunies au hasard, il n'y ait pas deux personnes qui aient leur anniversaire le même jour de l'année.
Le paradoxe des anniversaires, dû à Richard von Mises, est à l'origine une estimation probabiliste du nombre de personnes que l'on doit réunir pour avoir une chance sur deux que deux personnes de ce groupe aient leur anniversaire le même jour de l'année. Il se trouve que ce nombre est 23, ce qui choque un peu l'intuition. À partir d'un groupe de 57 personnes, la probabilité est supérieure à 99 %.
Cependant, il ne s'agit pas d'un paradoxe dans le sens de contradiction logique ; c'est un paradoxe, dans le sens où c'est une vérité mathématique qui contredit l'intuition : la plupart des gens estiment que cette probabilité est très inférieure à 50 %. ( ... )
Le problème des anniversaires revient à choisir un nombre n d'éléments dans un ensemble qui en comprend N, sans retrait ; c'est-à-dire sans retirer les éléments choisis, si bien que certains peuvent être identiques. Le paradoxe des anniversaires est bien un cas de ce type, car chacun a une date d'anniversaire plus ou moins aléatoire, et il n'y a pas a priori de raison autre que la probabilité pour que deux dates soit identiques ou différentes. ( ... )
Si l'on considère un nombre tiré donné, quelles sont ses chances d'être identique à un autre? Il peut être égal à n'importe quel autre ; en revanche, le nombre total de possibilités restreint ses chances : on a donc intuitivement une chance proportionnelle à 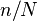 . Mais cette chance-là s'applique à tous les nombres tirés, si bien qu'au final la chance qu'un nombre tiré quelconque soit identique à n'importe quel autre nombre tiré est dans une proportion de
. Mais cette chance-là s'applique à tous les nombres tirés, si bien qu'au final la chance qu'un nombre tiré quelconque soit identique à n'importe quel autre nombre tiré est dans une proportion de  . C'est là que notre intuition est trompée.
. C'est là que notre intuition est trompée.
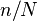 . Mais cette chance-là s'applique à tous les nombres tirés, si bien qu'au final la chance qu'un nombre tiré quelconque soit identique à n'importe quel autre nombre tiré est dans une proportion de
. Mais cette chance-là s'applique à tous les nombres tirés, si bien qu'au final la chance qu'un nombre tiré quelconque soit identique à n'importe quel autre nombre tiré est dans une proportion de  . C'est là que notre intuition est trompée.
. C'est là que notre intuition est trompée.
C'est là une grossière approximation valable seulement si n est bien plus petit que N. (Lorsque n grandit, ce raisonnement devient faux car un nombre de plus en plus grand de cas est compté plusieurs fois.) Mais cela donne néanmoins une idée des chances réelles et du point où notre appréciation intuitive est erronée : on s'attend à ce que la probabilité de coincidence soit en rapport de 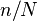 ; et donc « logiquement » qu'une probabilité de coincidence de 50 % soit grosso modo atteinte lorsque n est environ égal à N/2.
; et donc « logiquement » qu'une probabilité de coincidence de 50 % soit grosso modo atteinte lorsque n est environ égal à N/2.
Cela revient à dire que l’on confond la question posée : les chances de n’importe quel élément choisi d’être identique à n’importe quel autre, avec une autre question proche : les chances de n’importe quel élément choisi d’être identique à un autre élément donné. Dans le cas des anniversaires, on tend à évaluer intuitivement la probabilté pour que la date d’anniversaire de quiconque soit le même qu’une date d’anniversaire donnée (par exemple, la mienne) ; au lieu de la probabilité pour que la date d’anniversaire de quiconque soit la même que celle de n’importe qui d’autre.
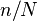 ; et donc « logiquement » qu'une probabilité de coincidence de 50 % soit grosso modo atteinte lorsque n est environ égal à N/2.
; et donc « logiquement » qu'une probabilité de coincidence de 50 % soit grosso modo atteinte lorsque n est environ égal à N/2.Cela revient à dire que l’on confond la question posée : les chances de n’importe quel élément choisi d’être identique à n’importe quel autre, avec une autre question proche : les chances de n’importe quel élément choisi d’être identique à un autre élément donné. Dans le cas des anniversaires, on tend à évaluer intuitivement la probabilté pour que la date d’anniversaire de quiconque soit le même qu’une date d’anniversaire donnée (par exemple, la mienne) ; au lieu de la probabilité pour que la date d’anniversaire de quiconque soit la même que celle de n’importe qui d’autre.
Reste à savoir pourquoi notre intuition est ainsi trompée, c’est-à-dire pourquoi elle ne semble pas spontanément capable d’aborder correctement un problème de ce type. C’est une question pour les sciences cognitives. ( ... )
Le plus simple pour obtenir le résultat annoncé est de calculer la probabilité que chaque personne ait un jour anniversaire différent de celui des autres : l’inverse de ce que l’on cherche. On va procéder par dénombrement, c'est-à-dire, que nous allons compter le nombre de cas où
 personnes ont des jours d'anniversaires différents et nous diviserons par le nombre de possibilités. Il y a
personnes ont des jours d'anniversaires différents et nous diviserons par le nombre de possibilités. Il y a  personnes, pour chacune il y a 365 jours possibles, donc au total si on ne se fixe aucune contrainte, il a
personnes, pour chacune il y a 365 jours possibles, donc au total si on ne se fixe aucune contrainte, il a 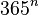 possibilités. Si maintenant on veut des jours différents, nous obtenons un arrangement de
possibilités. Si maintenant on veut des jours différents, nous obtenons un arrangement de  parmi 365, soit :
parmi 365, soit : 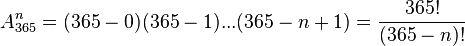 .
.
On a donc
Or, l'événement « un jour anniversaire différent par personne » est le complémentaire de « au moins deux identiques ». Par conséquent la probabilité recherchée est
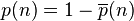 .
.
En faisant l'application numérique, on trouve 50,73 % pour vingt-trois personnes.
| n | p(n) |
|---|---|
| 5 | 2,71 % |
| 10 | 11,69 % |
| 15 | 25,29 % |
| 20 | 41,14 % |
| 23 | 50,73 % |
| 25 | 56,87 % |
| 30 | 70,63 % |
| 40 | 89,12 % |
| 50 | 97,04 % |
| 60 | 99,41 % |
| 80 | 99,99 % |
| 100 | 99,99997 % |
| 200 | 99,9999999999999999999999999998 % |
| 300 |  |
| 350 |  |
| > 366 | 100 % (par le principe des tiroirs) |

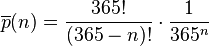

Aucun commentaire:
Enregistrer un commentaire