Le paradoxe de Simpson ou effet de Yule-Simpson est un paradoxe statistique décrit par Edward Simpson en 1951 et George Udny Yule en 1903, dans lequel le succès de plusieurs groupes semble s'inverser lorsque les groupes sont combinés. Ce résultat qui paraît impossible est souvent rencontré dans la réalité, en particulier dans les sciences sociales et les statistiques médicales.
Calculs rénaux : quel traitement choisir ?
Pas de chance, on vient de vous découvrir des calculs au rein. Heureusement des traitements existent, et à l’hopital le médecin vous en présente deux. Le premier (appelons le « Traitement A ») consiste en une chirurgie ouverte, alors que le second (« Traitement B ») est une chirurgie qui se fait par de petits trous percés à travers la peau. Le médecin vous demande quel traitement vous préférez. Comme vous souhaitez avant tout guérir, vous demandez au praticien les statistiques de succès de ces deux traitements.
« Oh c’est très simple, vous répond le médecin, les deux traitements ont été testés chacun 350 patients, et voici les chiffres : le traitement A a fonctionné dans 273 cas et le traitement B dans 289″.
L’affaire semble entendue, le traitement B a marché avec 83% de réussite, contre 79% seulement pour le traitement A. Vous choisissez donc le traitement B.
Mais en repartant de l’hôpital, vous croisez un autre médecin à qui vous demandez son avis sur les traitements. « Oh c’est très simple, vous répond-il : les deux traitements ont été testés 350 fois chacun sur des patients, ces derniers pouvant être atteints soit de ‘petits’ calculs, soit de ‘gros’ calculs, et voici les chiffres » :
Comme vous pouvez le constatez, si vous avez des gros calculs, le traitement A fonctionne mieux, et si vous avez des petits calculs, le traitement A est aussi le plus efficace. Voilà qui est en totale contradiction avec ce que vous a dit le premier médecin. Et pourtant, vous avez beau compter et recompter, sur la ligne « Total », il s’agit bien des mêmes chiffres que ceux présentés par le premier médecin…
Comment est-il possible que le traitement B soit meilleur au global, mais qu’il soit inférieur au traitement A aussi bien sur les petits que sur les gros calculs ? Et ça n’est pas une blague, ces chiffres sont issus d’une vraie étude [1] ! Il n’y a aucune entourloupe statistique ou aucune manipulation, ce que vous lisez là, c’est bien la réalité des chiffres. Vous avez là un bel exemple du paradoxe de Simpson. ( … )
Tout d’abord comment s’énonce ce paradoxe : il s’agit du fait qu’une corrélation peut disparaître ou même s’inverser suivant que l’on considère les données dans leur ensemble, ou bien segmentées par groupes.
Pour que le paradoxe se produise, il faut 2 ingrédients :
- Premièrement il faut une variable qui influe sur le résultat final (le « groupe »), et qui n’est pas forcément explicitée au départ. On appelle cela un facteur de confusion. Il s’agit de la taille des calculs dans le premier exemple, car celle-ci influe sur la probabilité de succès du traitement, et de l’âge des personnes dans le second exemple, lequel évidemment joue sur la mortalité.
- Deuxièmement, il faut que l’échantillon qu’on étudie ne soit pas distribué de manière homogène : dans le cas du tabac, il y a plus de vieilles femmes dans l’échantillon des non-fumeuses que chez les fumeuses; dans le cas des reins, le traitement « A » est plus souvent donné sur les gros calculs, et le « B » sur les petits (vous pouvez retourner voir les chiffres).
Quand ces deux conditions sont réunies, le paradoxe de Simpson peut se produire ! C’est-à-dire qu’à cause de la distribution hétérogène de l’échantillon, regrouper les données pointe une tendance qui peut être fausse, et qui disparaît si on analyse les données en séparant selon le facteur de confusion. ( … )
Comment se prémunir du paradoxe de Simpson
J’imagine que vous voyez aisément le potentiel de manipulation qui se cache derrière ce paradoxe : on peut vous faire croire à quelque chose (le chômage a baissé, tel traitement marche mieux, tel individu est meilleur, etc.) alors qu’en regardant les chiffres dans le détail, les effets peuvent disparaître ou s’inverser ! Alors que faire ?
Tout d’abord, il faut se rappeler : cet effet se produit quand il existe une variable cachée influente, et que l’échantillon sur lequel on se base n’est pas homogène. En sciences, c’est pour cela que l’on préfère en général des expériences « randomisées », qui permettent d’assurer une distribution homogène : par exemple si vous avez des calculs rénaux et que vous participez à une expérience pour comparer les traitements, on vous assigne au hasard le traitement A ou B, sans que la taille des calculs influe sur la décision. On gomme ainsi l’inhomogénéité de distribution, et le paradoxe disparaît : le traitement A sera bien vu comme étant le meilleur.
Quand on vous présente des chiffres, il faut donc avoir l’oeil critique, et être particulièrement méfiants quand ces chiffres sont issues de données analysées a posteriori, plutôt que sur un échantillon expérimental qu’on a soi-même construit a priori (en randomisant). (Réfléchissez au point suivant : conclure que « Le lit est l’endroit le plus dangereux du monde, c’est là que la plupart des gens meurent » c’est se tromper car on utilise des données non-randomisées)
Enfin rappelez-vous, ce paradoxe se produit quand il existe une variable cachée fortement influente. Cela signifie que les chiffres bruts ont peu de sens, et doivent être critiqués par un expert du domaine, susceptible de pointer l’existence d’un tel facteur. A l’heure où fleurit la mode du « fact-checking », on a un peu tendance à nous faire croire que les chiffres seraient la vérité « nue ». Non, la vérité nue n’existe pas, et on aura toujours besoin de gens au courant pour interpréter correctement des chiffres, qu’ils soient scientifiques, économiques ou médicaux.
https://sciencetonnante.wordpress.com/2013/04/29/le-paradoxe-de-simpson/
https://sciencetonnante.wordpress.com/2013/04/29/le-paradoxe-de-simpson/
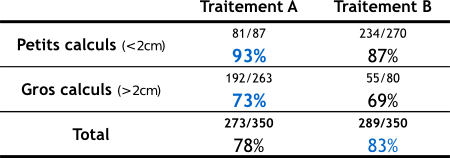
Aucun commentaire:
Enregistrer un commentaire