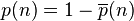Ce monde nous est prêté. Nous ne faisons qu’y passer, et au bout de peu de temps, nous laissons la terre, l’eau et l’air à ceux qui nous succèdent. Ma génération ‑ ou peut-être celle qui l’a précédée ‑ est la première à avoir livré à la nature une guerre coloniale exterminatrice sous la bannière des sciences.
L’avenir nous maudira pour cela.
Je ne pense pas qu’aucune organisation terroriste ait jamais demandé à la police fédérale de fixer des directives pour l’expérimentation correcte de bombes, mais je n’ai aucun doute quant à la réponse qu’elles auraient reçue, en l’occurrence de s’abstenir de tout acte répréhensible. Cela vaut également pour ce dont je voudrais parler ici : aucun rideau de fumée, aucun laboratoire de haute sécurité de type P3 ou P4 ne peut absoudre un chercheur s’il a fait du tort à un seul de ses prochains. Il me faut mettre mon espoir dans les femmes de ménage et les soigneurs employés dans les laboratoires où l’on joue avec des acides nucléiques recombinés, dans les juristes qui doivent reconnaître que la poursuite des erreurs médicales biologiques est une occasion en or, et dans les cours d’assises qui abhorrent toute espèce de docteurs.
En me battant, à l’instar de Don Quichotte, contre des moulins à vent pourvus du titre de «Dr med.», je m’attaquerai d’abord à la principale folie, à savoir le choix d’un hôte comme l’Escherichia coli. Voici ce qu’on lit à son propos dans un manuel de microbiologie apprécié: «E. coli est appelé colibacille, car il représente l’espèce prépondérante présente dans le tube digestif.» Nous hébergeons effectivement plusieurs centaines de variantes de cet utile micro-organisme. Il est responsable de quelques infections, mais sans doute de davantage de travaux scientifiques que tout autre organisme vivant. Si notre époque se sent appelée à créer de nouvelles sortes de cellules vivantes ‑ que notre monde n’a probablement jamais vues depuis qu’il existe ‑, pourquoi choisir un microbe qui vit avec nous depuis très longtemps avec plus ou moins de bonheur? Simplement parce que nous en savons bien plus sur l’E. coli que sur toute autre chose, y compris nous-mêmes. Mais est-ce une réponse valable? Prenez votre temps, faites bien vos recherches, et vous finirez par découvrir quantité de choses sur des organismes qui ne peuvent pas vivre dans le corps humain ou animal. Rien ne presse. ( ... )
S’il est vraiment indispensable que le Dr Frankenstein continue à fabriquer ses petits monstres biologiques ‑ ce dont je nie et l’urgence et la nécessité ‑, faut-il que cela se fasse au sein d’E. coli? C’est un domaine où chaque expérience est un coup tiré au hasard; qui peut savoir ce qui a pu être implanté en même temps dans l’ADN des plasmides que le bacille va multiplier jusqu’à la fin des temps? Et en fin de compte, malgré toutes les mesures de sécurité, cette chose finira par se retrouver dans l’organisme des hommes et des animaux. Il n’y a pas de véritable différence entre l’intérieur et l’extérieur. On nous assure certes que les travaux seront effectués avec des virus lambda affaiblis et des souches modifiées, défectueuses d’E. coli, qui ne peuvent vivre dans le tube digestif. Mais qu’en est-il de la modification du matériel génétique dans le tube digestif? Comment pouvons-nous être sûrs de ce qui arrivera une fois ces bestioles sorties du laboratoire? Voici ce qu’en dit le manuel déjà cité: «Il ne faut effectivement pas négliger l’éventualité qu’après recombinaison génétique, des bacilles intestinaux inoffensifs deviennent virulents.» Je pense pour ma part à quelque chose de plus grave que la virulence. Nous jouons avec le feu. ( ... )
Il reste cependant un problème capital qui dépasse tout cela de loin, le caractère irrévocable de cette entreprise. On peut abandonner la fission de l’atome, mettre un terme aux voyages sur la Lune; on peut s’abstenir d’utiliser des aérosols; on peut même imaginer que soit prise la décision de ne plus tuer des populations entières à l’aide de quelques bombes. Mais de nouvelles formes de vie ne peuvent revenir en arrière. Une cellule reconstruite et viable d’E. coli, véhiculant un ADN de plasmide où a été transplanté un fragment d’ADN eucaryote, vivra plus longtemps que nous et même que nos enfants. Cette attaque irréversible de la biosphère est une chose inouïe, impensable pour les générations précédentes, et je voudrais que notre génération ne s’en fût pas rendue coupable. L’abâtardissement de Prométhée et d’Erostrate ne peut que donner de mauvais résultats.
De fait, la plupart des résultats publiés à ce jour dans ce domaine sont peu convaincants. Nous en savons bien peu sur l’ADN eucaryote. Le sens des interruptions et des séquences fréquemment répétées dans l’ADN, de même que la fonction de l’hétérochromatine ne nous sont pas encore tout à fait clairs. On a l’impression que les essais consistant à inclure un fragment d’ADN animal dans l’ADN d’un plasmide microbien ont été faits sans qu’on sache exactement ce qui se passait. La place qu’occupe un gène donné dans l’ADN par rapport aux séquences de nucléotides voisines est-elle laissée au hasard ou bien résulte-t-elle d’un contrôle et d’une régulation réciproques? Pouvons-nous être sûrs ‑ pour ne citer qu’une improbabilité fantastique ‑ que le gène d’une hormone protidique donnée, qui ne fonctionne que dans certaines cellules spécialisées, ne devienne pas carcinogène s’il est introduit seul dans l’intestin? Est-il sensé de mélanger ce que la nature a séparé, à savoir les génomes de cellules eucaryotes et procaryotes?
Le pire est que nous ne le saurons jamais. En ce qui concerne l’homme, les bactéries et virus ont toujours fait partie d’un très puissant mouvement clandestin de la biologie. Il y a beaucoup de lacunes dans notre connaissance de la guérilla qu’ils livrent aux formes supérieures de vie. En ajoutant à cet arsenal des constructions de vie imprévisibles ‑ des procaryotes qui clonent les gènes eucaryotes ‑, nous jetons un voile d’incertitude sur la vie des générations futures. Avons-nous le droit de contrarier irrévocablement la sage évolution de millions d’années, pour satisfaire l’orgueil et la curiosité de quelques scientifiques?
Ce monde nous est prêté. Nous ne faisons qu’y passer, et au bout de peu de temps, nous laissons la terre, l’eau et l’air à ceux qui nous succèdent. Ma génération ‑ ou peut-être celle qui l’a précédée ‑ est la première à avoir livré à la nature une guerre coloniale exterminatrice sous la bannière des sciences.
L’avenir nous maudira pour cela.
Erwin Chargaff
Texte publié dans Le feu d’Héraclite, scènes d’une vie devant la nature, 1978 (trad. fr. éd. Viviane Hamy, 2006), pp. 292-297.
sniadecki.wordpress.com
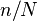. Mais cette chance-là s'applique à tous les nombres tirés, si bien qu'au final la chance qu'un nombre tiré quelconque soit identique à n'importe quel autre nombre tiré est dans une proportion de 
. C'est là que notre intuition est trompée.
personnes ont des jours d'anniversaires différents et nous diviserons par le nombre de possibilités. Il y a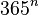 
possibilités. Si maintenant on veut des jours différents, nous obtenons un 
.
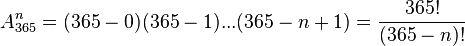